Übersetzungen aller Art einfach berechnet
Die Welt der Drehzahl im Griff
Drehmomente können auf verschiedene Weise übertragen werden. Das kann über Seile, Ketten oder Zahnräder geschehen. Oft soll dies jedoch kontrolliert erfolgen. Beispielsweise soll das Drehmoment vergrößert und dabei auch gleich eine große Strecke überwunden werden. Maschinenkonstrukteure benötigen daher eine gut gefüllte Lösungstruhe, um zu jeder Aufgabe das passende Rezept anzuwenden.

Kettentriebe sind wohl jedem bekannt, schließlich hat jedes Fahrrad so ein System, das die Kraft der Beine auf den Hinterreifen bringt. Wer sich die Machart dieser Technik einmal näher ansieht, bemerkt, dass an den Pedalen sich größere Kettenblätter befinden, als am Hinterrad. Dies hat den einfachen Grund, dass durch diese Anordnung der Fahrer mit den Pedalen nur wenige Umdrehungen machen muss, am Hinterrad jedoch wesentlich mehr Umdrehungen erfolgen. Auf diese Weise kann mit einer Umdrehung der Tretkurbel ein großer Fahrweg mit dem Rad zurückgelegt werden.
Problematisch wird es am Berg, wo eine relativ große Kraft nötig wird, um das Rad mitsamt dem aufsitzenden Fahrer auf den Berg zu bekommen. Hier sind Kettenschaltungen vorteilhaft, da nun vorne die Kette auf ein kleineres Kettenblatt umgelegt werden kann, während hinten ein größerer Zahnkranz am Zahnkranzpaket gewählt wird. Dadurch wird zwar bei einer Umdrehung der Tretkurbel weniger Weg mit dem Rad zurückgelegt, die aufzubringende Kraft nimmt jedoch dramatisch ab, sodass nun das Bergauffahren möglich wird. Am Fahrrad kann man also die Wirkung von Übersetzungen hautnah spüren.
Dieses Verständnis ist wichtig. Es erleichtert den Zugang zum Berechnen von Übersetzungen von Ketten- oder Riementrieben sowie von Zahnrädern. Während Ketten- und Riementriebe ideal dafür geeignet sind, größere Entfernungen zwischen der getriebenen und der angetriebenen Welle zu überbrücken, sind Zahnräder ideal, wenn es darum geht, präzise Drehzahlen zu erreichen. Uhren zum Beispiel wären mit Ketten- oder Riementrieben viel zu ungenau, ganz zu schweigen von den technischen Problemen, wenn es um kompakte Bauweise geht.
In diesem Kurs geht es um die Berechnung verschiedener Übersetzungen. Es wird gezeigt, dass es problemlos möglich ist, eine Maschine zu bauen, bei der das letzte Rad nahezu unbeweglich verharrt, während das erste angetriebene Rad mit 600 Umdrehungen pro Minute richtig Gas gibt. Dies wurde im Mittelalter als Hexenwerk angesehen, weshalb damalige Techniker gut daran taten, ihre Innovation nur im Verborgenen einem ausgewählten Interessentenkreis zu zeigen.
Womöglich ist dieses Versteckspiel mit ein Grund, warum es zunächst lediglich Hoch- beziehungsweise Laufräder gab, die ohne Übersetzungseinrichtung auskommen mussten. Zu bedenken ist auch, dass Zahnräder schon in der Antike bekannt waren, wie nicht zuletzt die Zahnradmaschine von Antikythera zeigt. Die Entstehungszeit des Geräts wird auf 205 v. Chr. geschätzt. Es wird vermutet, dass der Sternenrechner höchstwahrscheinlich auf babylonischer Mathematik beruht. Wer also Übersetzungsverhältnisse berechnen kann, hält auch den Schlüssel zu höchst interessanten Maschinen in der Hand.
Einfache Übersetzung mit Riementrieb
Die einfache Übersetzung ist beispielsweise beim Fahrrad gegeben. Es soll das Übersetzungsverhältnis bei einer bestimmten Kettenblatt-Zahnkranz-Kombination ermittelt werden.
Beispiel:

Das Verhältnis bedeutet, dass 0,6 Umdrehungen am Kettenblatt eine ganze Umdrehung am Zahnkranz zur Folge hat. Umgerechnet bedeutet dieses Verhältnis, dass eine Umdrehung am treibenden Rad (Kettenblatt) 1,64 Umdrehungen am getriebenen Rad (Zahnkranz) ergeben. Dabei spielt es keine Rolle, wie weit die beiden Räder voneinander entfernt sind. Ketten können nahezu beliebig lang sein, da diese aus einzelnen Segmenten zusammenmoniert werden, um jede Distanz zu überbrücken.
Würde ein Fahrradfahrer pro Minute 100 Mal die Tretkurbel drehen, so würde sich der Zahnkranz mit 164 Umdrehungen pro Minute drehen. Hat der Reifen einen Umfang von zum Beispiel 2110 mm, so würde sich das Fahrrad dadurch um 164x2110 mm, also circa 346 Meter weiterbewegen. Der Radler ist; somit mit 346x60=circa 20 km pro Stunde unterwegs.
Natürlich könnte man nun vorne ein größeres Kettenblatt oder hinten einen kleineren Zahnkranz einbauen, um mit der gleichen Drehfrequenz der Tretkurbel ein höheres Tempo zu erreichen. Angenommen, man will 30 km/h bei 100 Umdrehungen erreichen so muss zurückgerechnet werden:
Zurückgelegte Strecke pro Minute: 30.000:60=500 Meter/Min.
Nötige Umdrehungen des Zahnkranzes: 500.000 mm:2110 mm = 237 U/min.

Um mit 100 Umdrehungen in der Minute auf eine Geschwindigkeit von 30 km/h zu kommen, müsste also ein Kettenblatt mit einem Durchmesser von 187 mm an die Tretkurbel montiert werden. Ob der Fahrer allerdings die dafür nötige Kraft auf Dauer aufbringen kann, ist eine ganz andere Frage.
Mehrfache Übersetzung mit Riementrieb
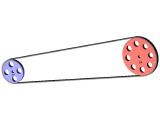
Mehrfache Übersetzungen erlauben praktisch das unbegrenzte Manipulieren von Drehzahl und übertragenes Drehmoment mit der Möglichkeit, an unterschiedlichen Stellen im Getriebe verschiedene Drehzahlen und Drehmomente abzugreifen. Mit einem Riementrieb können dabei große Entfernungen überbrückt werden. Die Berechnungen bezüglich Drehzahl, Übersetzungsverhältnis oder gesuchtem Raddurchmesser sind grundsätzlich identisch zur Vorgehensweise bei einfachen Übersetzungen. Der Unterschied liegt lediglich in der Berücksichtigung aller treibenden beziehungsweise getriebenen Räder in den Formeln.
In folgendem Beispiel soll an der letzten angetriebenen Scheibe d4 eine Drehzahl von 400-1 anliegen. Weiterhin gelten folgende Werte:

Gesucht wird also der Durchmesser d4 der letzten Scheibe. Zur Vervollständigung wird auch gleich das Gesamtübersetzungsverhältnis berechnet. Dieses wird diesmal aus den bekannten Drehzahlen berechnet, da die Scheibendurchmesser nur zum Teil bekannt sind, das Gesamtübersetzungsverhältnis zum jetzigen Zeitpunkt daher aus diesen noch nicht berechenbar ist.

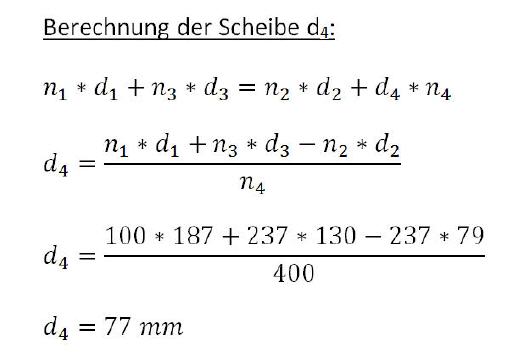
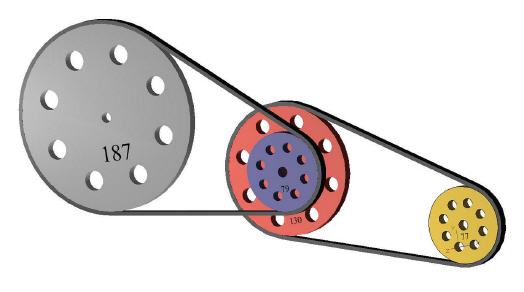
Übrigens: Wer Probleme mit dem Formelumstellen hat, kann sich einen CAS-Taschenrechner besorgen – etwa den NSpire CAS von Texas Instruments – der diese Funktion bietet.
Zahnradübersetzungen für Uhrwerke berechnen
Das eben Gelernte ist wunderbar geeignet, sich dem Geheimnis der Uhrmacherkunst zu nähern. Es spielt schließlich keine Rolle, ob Übersetzungen mit Ketten, Seilen, Riemen oder eben mit Zahnrädern umgesetzt werden. Zahnräder sind zwar aufwendiger herzustellen beziehungsweise zu besorgen, doch wesentlich präziser im Lauf.
Ein absolut empfehlenswerter Weg, sich der Funktionsweise eines Uhrwerks zu nähern, ist der Kauf einer Spielzeuguhr, die sehr preiswert etwa vom Versandhändler Pearl zu beziehen sind. Die Zahnräder dieses Uhrwerks sind bunt eingefärbt und das Gehäuse ist durchsichtig, sodass der Lauf der Zahnräder bestens verfolgt werden kann. Noch besser ist allerdings, dass die Uhr zerlegt angeliefert wird, sich daher optimal für eigene Versuche und Berechnungen eignet.
Die im Bausatz vorhandenen Zahnräder haben folgende Merkmale:
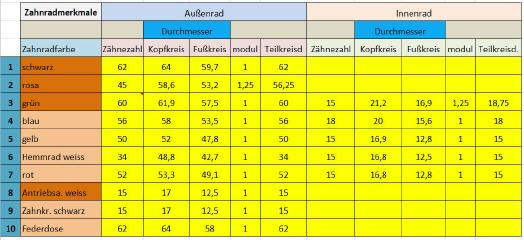
Mit den Merkmalen ›Innenrad‹ und ›Außenrad‹ wird bei Zahnrädern mit zwei Verzahnungen deren Verzahnung aufgeschlüsselt. Dabei ist mit ›Innenrad‹ das kleinere Zahnrad gemeint.
Mit dem mitgelieferten Montageplan ist es sehr einfach, die Uhr zusammenzubauen. Dabei fällt sofort ins Auge, dass der Kraftfluss, der von der Federdose ausgeht, zwei Richtungen nimmt. Einmal wandert das Drehmoment über mehrere Zahnräder zum Hemmrad und einmal zum eigentlichen Zahnradverbund, der für die Uhrzeitanzeige zuständig ist.

Funktionsweise der Kraftübertragung zum Pendel
Der Kraftfluss zum Hemmrad hat eine raffinierte Aufgabe: Auf diese Weise wird verhindert, dass die Federkraft in der Federdose in zu kurzer Zeit in das für die Uhrzeitanzeige wichtige Getriebe eingeleitet wird.
Dabei wird zunächst über das Hemmrad diese Kraft über die sogenannte Hemmung an ein Pendel weitergeleitet, das durch die dort eingeleitete Energie in eine Pendelbewegung versetzt wird. Diese sorgt dafür, dass wiederum das Hemmrad über die Hemmung kontrolliert getaktet weiterbewegt wird. Wäre das Pendel nicht vorhanden, würde die Hemmung das Hemmrad blockieren und dessen Drehbewegung würde zum Stillstand kommen.
Wäre auch noch die Hemmung nicht vorhanden, würde das Hemmrad sogar durchdrehen, bis die in der Federdose gespeicherte Energie aufgebraucht wäre. In der Folge würden Stunden- und Minutenzeiger sehr schnell ihre Kreise drehen und eine sinnvolle Zeitanzeige wäre unmöglich. So aber wird die Federdose mit dem dort vorhandenen Zahnrad nur sehr langsam bewegt, was es erlaubt, über das zweite Getriebe die Zeit genau anzuzeigen.
Die passende Drehzahl der Federdose
Eine genaue Betrachtung der Funktionsweise dieser Uhr zeigt, dass die Kraft von der Federdose über das Schwarze Zahnrad auf das Getriebe übertragen wird, das für die Anzeige der Uhrzeit zuständig ist. Dabei zeigt sich, dass das in das schwarze Zahnrad fest eingepresste weiße Zahnrad für die Drehung des Minutenzeigers zuständig ist. Das rosafarbige Zahnrad wird dabei nicht mitbewegt. Es hat keine feste Verbindung zum weißen Zahnrad, was durch eine große Spielpassung zwischen Bohrung und Welle der beiden Zahnräder ermöglicht wird.
Dies bedeutet, dass sich das schwarze respektive das weiße Zahnrad genau mit einer Umdrehung pro Stunde drehen müssen, damit ein auf dem weißen Zahnrad angebrachter Minutenzeiger genau ein Mal pro Stunde eine Bewegung um 360 Grad ausführen kann. Das macht der Minutenzeiger zwölfmal, wodurch sich der Stundenzeiger einmal um 360 Grad dreht.
Wie ein Blick in die obige Tabelle zeigt, wird dies durch die identische Zähnezahl (62) sowie dem identischen Teilkreis (62 mm) erreicht.

Die Drehbewegung des Stundenzeigers
Nachdem nun feststeht, dass der Minutenzeiger praktisch direkt die Drehbewegung der Federdose abbildet, ist es interessant zu erfahren, auf welchem Weg der Stundenzeiger zur Einhaltung der passenden Drehfrequenz angehalten wird.
Die Betrachtung des Uhrwerks zeigt, dass das Drehmoment vom weißen Zahnrad auf den großen Zahnkranz des grünen Zahnrads übertragen wird. Von dort wird es über den kleinen Zahnkranz auf das rosafarbige Zahnrad übertragen, auf dessen Zapfen der Stundenzeiger mittels Presspassung eingefügt ist.
Interessant ist nun die Berechnung der Übersetzung, damit der Stundenzeiger korrekt seine Kreise ziehen kann.
Würde sich der Stundenzeiger an anderer Stelle der Uhr bewegen, so könnte man das Problem mit nur einem Zahnradpaar lösen. Angenommen, der Stundenzeiger wäre auf dem grünen Zahnrad fixiert und würde sich mit diesem mitdrehen, so wäre ein sehr großes grünes Zahnrad nötig, das gar nicht in das sowieso schon großzügige Gehäuse der Spielzeuguhr passen würde.

Zum Durchrechnen dieses Falls wird angenommen, dass das vorhandene weiße Zahnrad mit einem Teilkreisdurchmesser von 15 mm als treibendes Rad verwendet wird. Die Rechnung lautet:
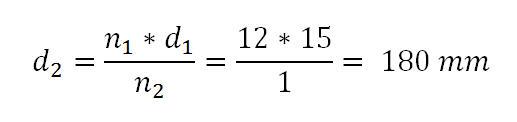
Der Stundenzeiger würde demnach praktisch am Gehäuserand seine Kreise ziehen. Das Übersetzungsverhältnis würde lauten:
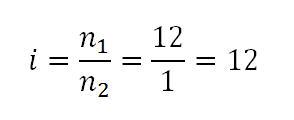
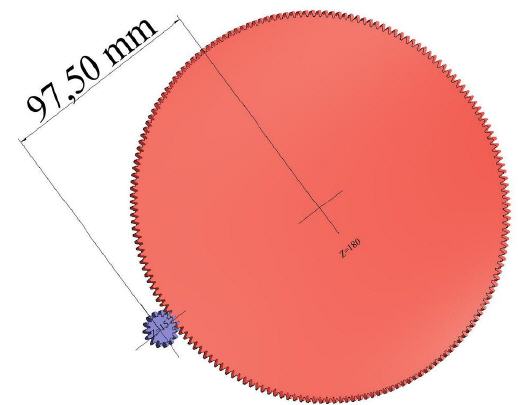
Damit ist klar, dass der Weg über weitere Zahnradübersetzungen beschritten werden muss, um zum gewünschten Ergebnis bei begrenztem Platz zu kommen.
Die Grundüberlegung für ein Uhrwerk ist, dass der Stundenzeiger in zwölf Stunden eine Umdrehung macht, während der Minutenzeiger in der gleichen Zeiteinheit 12 Umdrehungen macht.
Nun gibt es die Möglichkeit, den zur Verfügung stehenden Achsabstand der Zahnräder als Rechengrundlage zu nehmen, um das hier umsetzbare Größenverhältnis der Zahnräder zu bestimmen. Die Speilzeuguhr hat einen Achsenabstand von 38 Millimeter. Daher soll mit diesem Wert gearbeitet werden, die Zahnräder zu ermitteln, die für ein funktionierendes Uhrwerk nötig sind.
Eine mögliche Lösung lautet wie folgt:
Gegeben: Drehzahl n1=12
Zwischendrehzahl n2=4
Zwischendrehzahl n3=n2
Enddrehzahl n4=1
Achsabstand a=38 mm
Aus diesen Angaben kann über das notwendige Übersetzungsverhältnis auf die zu wählenden Teilkreisdurchmesser der Zahnräder geschlossen werden.

Da das Übersetzungsverhältnis ›i‹ nicht nur das Verhältnis zwischen den Drehzahlen, sondern auch das Größenverhältnis der beiden im Eingriff stehenden Zahnräder angibt, können damit problemlos die Durchmesser der beiden Zahnräder ermittelt werden. Wichtig ist dabei die Berücksichtigung der Mengenanteile der Zahnräder an den Drehzahlen.
Im obigen Fall ist das getriebene Rad drei Mal langsamer, als das treibende Rad. Zusammen besitzen beide Räder vier Anteile, die auf den Achsabstand ›a‹ aufgeteilt werden müssen! Diese Erkenntnis ist wichtig um die Berechnung der Zahnrad- beziehungsweise Teilkreisdurchmesser zu verstehen.

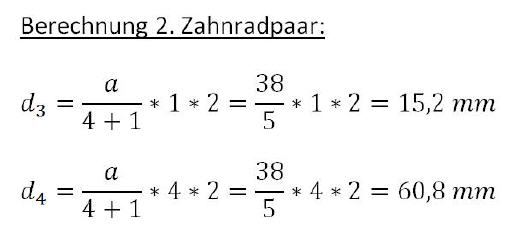
Dieses Ergebnis liegt bereits recht nahe an den tatsächlich verwendeten Zahnrädern der Spielzeuguhr, wie obige Tabelle verdeutlicht. Eine mit diesen Werten aufgebaute Uhr würde problemlos funktionieren.
Solche Berechnungen kann man sehr bequem mit der zum Download bereitgestellten Excel-Tabelle durchführen.
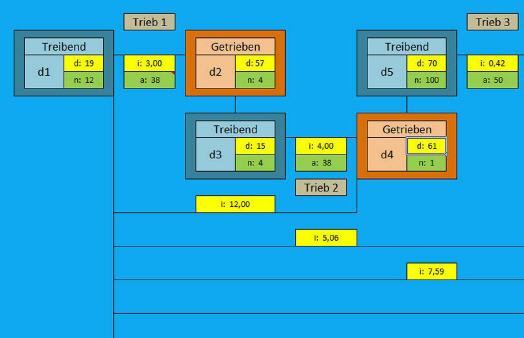
Eine Berechnung mit den tatsächlich vorhandenen Zahnrädern klärt, wie genau die Uhr mit diesen Rädern die Zeit anzeigen kann.



Wie das Ergebnis zeigt, ist das ideale Übersetzungsverhältnis von 12:1 zwischen dem schwarzen und dem rosafarbenen Rad erreicht worden, mithin funktioniert die Spielzeuguhr rein rechnerisch perfekt. Das schwarze Rad treibt über die weiße Steckachse den Minutenzeiger an, während der Stundenzeiger über das rosafarbene Rad in der richtigen Geschwindigkeit angetrieben wird. Die nötige Reduzierung der Drehzahl wurde über das weiße beziehungsweise grüne Rad vorgenommen.
Kleine Gangabweichungen können durch eine Längenänderung des Pendels entlang der Pendelachse ausgeglichen werden, denn mit der Schwingfrequenz des Pendels wird die Drehgeschwindigkeit der Federdose beeinflusst, die schließlich das eigentliche Uhrwerk antreibt.
Fazit:
Wer mit Zahnrädern zu tun hat, etwa als Azubi oder Student das Berechnen von Getrieben lernen muss, der sollte sich daher eine günstige Spielzeuguhr besorgen, und damit derartige Übersetzungsberechnungen üben. Der damit erzielte Lerneffekt ist unbezahlbar.
Auch sollte nicht versäumt werden, sich die Excel-Tabelle zum Berechnen von Übersetzungen herunterzuladen. Mit deren Hilfe wird das Berechnen von Uhren aller Art zum Vergnügen und sogar selbst gebaute Planetarien bleiben kein Traum mehr.
Hinweis:
In einer früheren Version dieses Artikels wurde versehentlich angenommen, dass das grüne Zahnrad 58 statt 60 Zähne hätte. Daher wurden die nachfolgenden Berechnungen falsch vorgenommen. Dieser Fehler wurde von einem aufmerksamen Leser bemerkt, dem wir hiermit danken möchten. Die Berechnungen wurden korrigiert.

Download:
Die Excel-Tabelle zur Berechnung von Übersetzungen können Sie hier herunterladen [54 KB] .
Video:
Mehr Informationen:
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 9 - gesamt: 14793.