Wechselradberechnung leichtgemacht
Via Excel schnell zum gewünschten Gewinde
Eigner moderner Universaldrehmaschinen müssen sich in der Regel nicht mehr mit dem Berechnen von Wechselrädern auseinandersetzen. Heutige Universaldrehmaschinen haben entweder einen wohldurchdachten Getriebeaufbau, mit dem alle üblichen Steigungen herstellbar sind oder sind sogar mit einer entsprechenden Steuerung ausgestattet, die per Knopfdruck die Antriebsmotoren der Drehmaschine entsprechend synchronisiert, um selbst exotische Gewindewünsche zu erfüllen. Doch ist das Wechselradberechnen noch nicht aus der Mode gekommen, da es immer noch Drehmaschinen-Oldtimer in so mancher Werkstatt gibt. Eine Excel-Tabelle hilft, das Berechnen zu vereinfachen.

Wer eine Universaldrehmaschine sein Eigen nennt, die bereits viele Jahrzehnte gute Dienste leistet, wird diese nicht entsorgen, wenn dann und wann Gewinde mit Steigungen zu drehen sind, die nicht per einfachem Einstellen, des Wechselradgetriebes anwählbar sind. In diesem Fall sind neue Wechselräder aufzustecken, die dafür sorgen, dass auch Gewinde abseits des Üblichen herstellbar sind.
Wechselräder sind dazu da, die Drehbewegung der Arbeitsspindel derart umzusetzen, dass die Leitspindel um den exakt passenden Betrag weitergedreht wird. Dadurch wird der Drehmeißel um die Steigungslänge weiterbewegt, wenn sich das Werkstück einmal um sich selbst dreht.
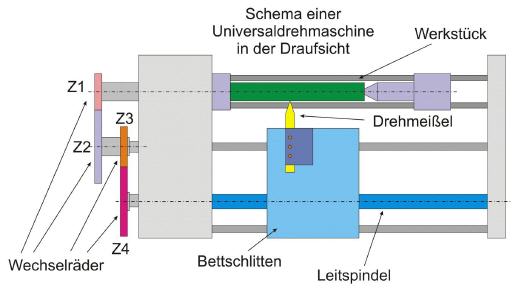
Universaldrehmaschinen haben üblicherweise eine Zug-, sowie eine Leitspindel. Die Leitspindel ist mit einem Trapezgewinde versehen und wird nur dann zum Bewegen des Bettschlittens verwendet, wenn es darum geht, ein Gewinde in ein Drehteil einzubringen. Für alle anderen Arbeiten wird die Zugspindel verwendet, um die Leitspindel zu schonen.
Soll nun ein Gewinde geschnitten werden, so wird die Zugspindel außer Eingriff gebracht und eine zweigeteilte Mutter – die als Schlossmutter bezeichnet wird und ebenfalls mit einem Trapezgewinde versehen ist – in das Gewinde der Leitspindel eingeschwenkt. Durch den Formschluss zwischen Schlossmutter und Leitspindel sowie den Kraftfluss über die Wechselräder wird eine exakte Synchronisierung zur Drehbewegung des Werkstücks erreicht.
Muss ein Gewinde geschnitten werden, dessen Steigung nicht direkt an der Universaldrehmaschine einstellbar ist, so müssen alternative Wechselräder aufgesteckt werden, die derart abgestimmt sind, dass eine Umdrehung des Werkstücks einer bestimmten Positionsänderung des Bettschlittens entspricht. Diese Positionsänderung, auch Versatz genannt, entspricht der Steigung des Werkstücks.
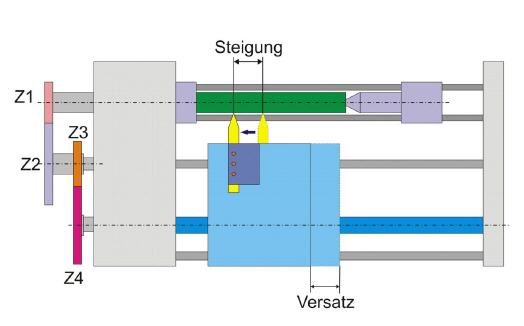
Die Wechselradberechnung:
Zur Berechnung der passenden Wechselräder ist eine recht einfache Formel nötig. Diese lautet:
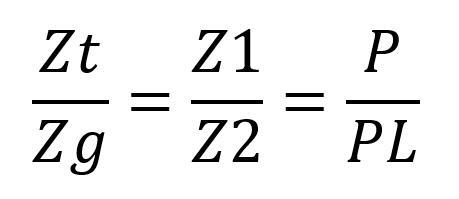
Es bedeuten:
Zt: Zähnezahl des treibenden Rades
Zg: Zähnezahl des getriebenen Rades
P: Steigung des zu schneidenden Gewindes
PL: Steigung der Leitspindel
Die Kunst besteht nun darin, die Bruchrechnung dergestalt durchzuführen, dass dabei jeweils Zahlen als Nenner beziehungsweise Zähler als Ergebnis herauskommen, die auch in der verwendeten Wechselradtabelle vorkommen. Diese könnte beispielsweise lauten:
20, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 97, 100, 105, 110, 115, 120, 127
Besitzt nun die Leitspindel eine Steigung von sechs Millimeter und es soll am Werkstück ein Gewinde mit einer Steigung von zwei Millimeter geschnitten werden, so ist folgende Rechnung anzustellen:
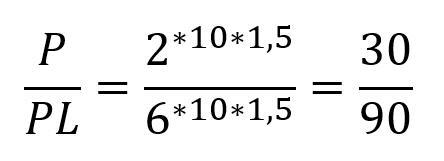
Nach dieser Berechnung müssten zwei Wechselräder mit 30 beziehungsweise 90 Zähnen verwendet werden, um das Gewinde mit der gewünschten Steigung zu schneiden. Diese Wechselräder kommen auch in der Wechselradtabelle vor. Dies bedeutet, dass diese Wechselräder vorhanden sind, somit das Gewinde durch Aufstecken dieser Räder geschnitten werden kann.
Eine alternative Berechnung:
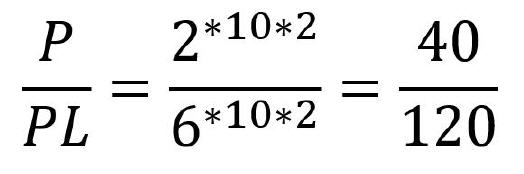
Wechselräder mit 40 beziehungsweise 120 Zähnen sind ebenfalls im Wechselradsatz vorhanden. Diese Wechselräder sind demnach ebenfalls geeignet, mit einer Leitspindel von sechs Millimeter Steigung ein Gewinde in ein Werkstück zu schneiden, das eine Steigung von zwei Millimeter besitzen soll.
Umsetzung mit Excel:
Das Berechnen von Wechselrädern ist mit einigem Zeitaufwand verbunden, weshalb sich hier eine Tabellenkalkulation, wie etwa Excel anbietet, für Erleichterung zu sorgen. Die zum Download bereitgestellte Variante berechnet rasch jede Wechselradkombination, die zur gewünschten Steigung am Werkstück führt.

Wechselradberechnung mit Excel:
In obigem Bild wird das Ergebnis der bereits besprochenen Aufgabe dargestellt.
Nun kann es passieren, dass für eine Steigung keine passenden Wechselräder vorhanden sind, weil diese wegen der dazu nötigen Größe nicht montierbar wären. Beispielsweise würden für eine Steigung von einem Millimeter folgende Wechselräder benötigt werden:
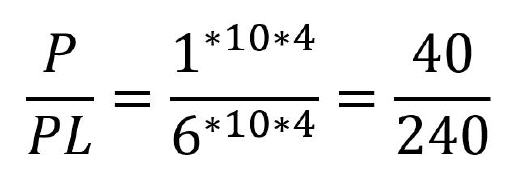
Zwar wäre ein 40er Rad vorhanden, doch kein 240er Rad. Ein Wechselrad mit dieser Zähnezahl würde sich wegen seiner Größe nicht montieren lassen. Folglich ist es daher nicht im Rädersatz aufgeführt. Vor diesem Platzproblem stehen nicht zuletzt Uhrenbauer, die diese Knacknuss durch die Nutzung mehrerer Zahnräder umgehen. Dadurch bleiben die Zahnräder klein, wodurch Uhrengehäuse kompakter ausfallen können.
Werden mehrere Wechselräder benötigt, ist deren Bestimmung unter Umständen eine längere Rechnerei, wenn manuell gerechnet wird. Um nun eine Tabellenkalkulation für die Berechnung verwenden zu können, ist es ratsam, die zum Erreichen der korrekten Werkstücksteigung nötigen Umdrehungen der Leitspindel in Grad zu bestimmen. Dazu ist immer zu bedenken, dass das Werkstück beziehungsweise die Arbeitsspindel stets eine volle Umdrehung ausführen müssen, damit die jeweilige Steigung korrekt abgebildet wird.
Dies gilt unabhängig davon, welche Steigung das Gewinde des Werkstücks schlussendlich bekommen soll! Alleine der zurückzulegende Winkel an der Leitspindel ist der entscheidende Faktor, damit der Bettschlitten exakt um die gewünschte Steigung verfahren wird.
Konkret bedeutet dies: Um am Werkstück eine beliebig große Steigung herzustellen, muss sich die Arbeitsspindel beziehungsweise das Werkstück stets um 360 Grad drehen, damit diese Steigung erreicht wird. Die Leitspindel hingegen darf sich nur um einen bestimmten Winkel weiterbewegen, der alleine von der Steigung der Leitspindel abhängt. Beträgt die Leitspindelsteigung beispielsweise sechs Millimeter und es ist ein Gewinde mit einer Steigung von einem Millimeter zu schneiden, so beträgt der einzuschließende Winkel für die Leitspindel:
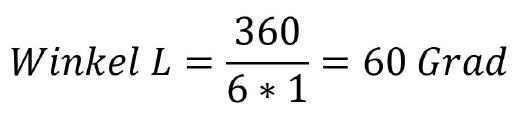
Ein Bild verdeutlicht das Schema:
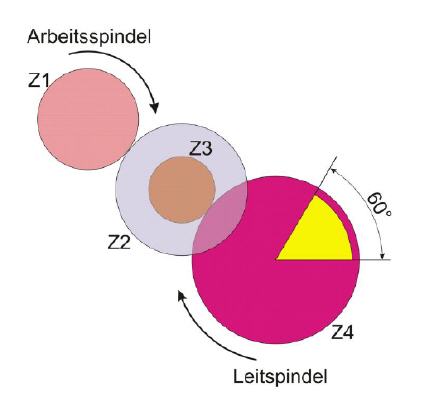
Nun greift der klassische Dreisatz: Wird die Leitspindel um 360 Grad gedreht, so bewegt sich der Bettschlitten um sechs Millimeter weiter, da die Leitspindel eine Steigung von sechs Millimeter hat.
Bei einem Winkel von 60 Grad verbleiben davon:
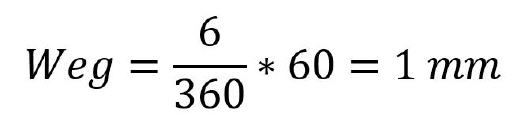
Wird die Leitspindel um 60 Grad gedreht, so bewegt sich der Bettschlitten demnach exakt um einen Millimeter weiter, wodurch der Gewindedrehmeißel ein Gewinde mit der gewünschten Steigung schneiden kann.
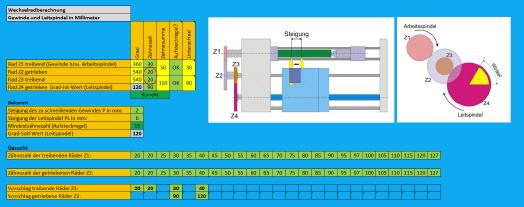
Eine korrekte Wechselradkombination wäre demnach beispielsweise Lösung 1:
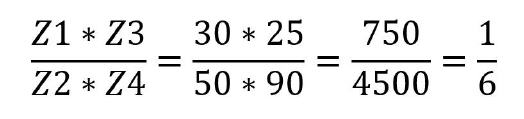
Eine alternative Kombination wäre beispielsweise Lösung 2:
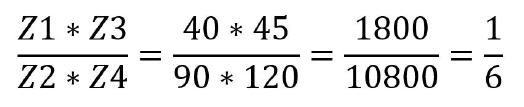
In beiden Fällen wird das Gewinde am Werkstück mit der korrekten Steigung geschnitten. Zu beachten ist, dass die Excel-Tabelle in diesem Fall nicht für eine automatische Berechnung der Zahnräder ausgelegt ist. Dies ist auch nicht nötig, da man die passenden Zahnräder sehr rasch durch Ausprobieren ermitteln kann: Einfach die in der Wechselradtabelle zur Verfügung stehenden Zähnezahlen einsetzen und immer die Regel vor Augen halten, dass die Kombination ›kleines treibendes Zahnrad und großes getriebenes Zahnrad‹ zu kleineren Drehzahlen führt, während die Kombination ›große treibendes Zahnrad und kleines getriebenes Zahnrad‹ zu einer Drehzahlerhöhung führt.
Dies bedeutet, dass sich so auch der Winkel an der Leitspindel durch die Wahl der Wechselräder entsprechend ändern lässt. Eine Lösung ist durch Probieren in der Regel rasch gefunden.
Nun gibt es jedoch noch die sogenannte Aufsteckregel zu beachten. Diese besagt, dass die Gesamtzähnezahl von Z1+Z2 um mindestens 15 größer sein muss, als die Zähnezahl von Z3. Darüber hinaus muss die Gesamtzähnezahl von Z3+Z4 um mindestens 15 größer sein, als die Zähnezahl von Z2.
Prüfung von Lösung 1:
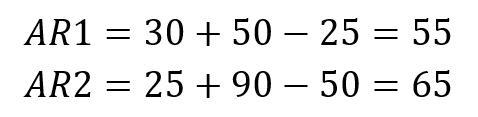
Prüfung von Lösung 2:
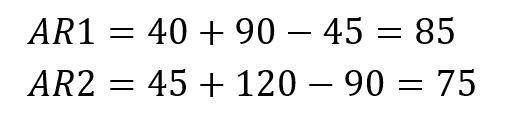
In beiden Fällen liegen die Räderkombinationen deutlich über der Mindestgröße von 15, können also problemlos genutzt werden.
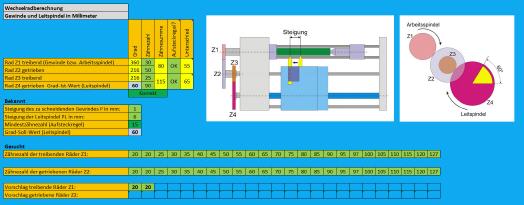
Übrigens: Wer nochmals das Beispiel mit einer Steigung von zwei Millimeter mithilfe der Excel-Tabelle durchrechnet, wird feststellen, dass für Z2 und Z3 jeweils ein Zahnrad mit 20 Zähnen nötig ist, um die Fehlermeldung „Unpassend“ zu verhindern. In diesem Fall zeigt sich, dass zwei gleichartige Zahnräder die Drehzahl 1:1 weitergeben. Solange nicht explizit vier Wechselräder benötigt werden, sind diese als technische Hilfe beziehungsweise zur Kraftweiterleitung nötig.
Download:
Unter nachfolgendem Button können Sie sich eine Excel-Tabelle herunterladen, die das Berechnen von Wechselrädern ermöglicht.
War dieser Artikel für Sie hilfreich?
 |
 |
 |
 |
 |
Bitte bewerten Sie diese Seite durch Klick auf die Symbole.
Zugriffe heute: 1 - gesamt: 23510.